Linear Actuator - Velocity Control
This guide explains the basics of PID control and how to implement a basic control loop using Phidgets
by Mike

A linear actuator is a motor that has been geared to extend and contract an arm rather than rotate a shaft. Many applications that use linear actuators require precise position control, but since DC motors can ordinarily only be told how fast to go (on a scale from -100% and 100% duty cycle) you need to program a control system. In order to make a control system, you'll need a linear actuator that has a built-in feedback device such a as a potentiometer.
Introduction
This application guide will go through the steps to create a velocity control loop for your linear actuator. A properly written velocity control loop will ensure that the actuator reaches the target position while attempting to move at the desired velocity. This means that even if the actuator encounters some external resistance, it will adjust and increase the duty cycle until it is moving at the appropriate velocity. This guide builds upon the control techniques described in the PID Control of a Linear Actuator guide, so you may want to try that example before this one.
Phidgets
The following setup was used to build this application guide:
You could use the 1064_1 - PhidgetMotorControl HC instead, but it doesn't have an analog input for the feedback device, so you'd also need to use a device with an analog input and change the program accordingly in this case. The soldering kit is used to split the actuator connector into a Phidget cable and a pair of motor wires. You could also use a solderless breadboard to accomplish this.
Velocity Control
The implementation of a velocity control loop is similar to the position control of a PID control loop. However, instead of comparing current position with target position, we will instead compare current (estimated) velocity with target velocity. Target velocity is calculated from the difference between the target position and current position, and limited by the user-defined velocity limit. Each iteration of the control loop will compare current velocity against the target velocity, constantly making adjustments to the duty cycle. In a similar structure to the PID algorithm, we will add multiple terms together, each weighted by a control gain to allow tuning of the system.
Proportional Control

Just like the Proportional Control in the PID example, the proportional term in a velocity control loop simply compares current velocity with the target. For example, we could implement proportional control by calling the following function in the potentiometer change handler:
void ControlLoop()
{
// Update position array and variables
for (int i = 63; i > 0; i--)
{
positionArray[i] = positionArray[i-1];
}
positionArray[0] = positionCurrent;
positionOld = positionArray[63];
// Update velocity variables
velocityCurrent = (positionCurrent - positionOld) / (64 * dt);
velocityTarget = (positionTarget - positionCurrent) * Kv;
// Limit target velocity to the user-specified amount
if (velocityTarget >= maxOutput)
velocityTarget = maxOutput;
if (velocityTarget <= -maxOutput)
velocityTarget = -maxOutput;
// Update error values
velocityError = velocityTarget - velocityCurrent;
positionError = positionCurrent - positionTarget;
// If the error is within the specified deadband, and the motor is moving slowly enough
// Or if the motor's target is a physical limit and that limit is hit
// (within deadband margins),
if ((Math.Abs(positionError) <= deadBand && Math.Abs(output) < 5)
|| (positionTarget < (deadBand + 1) && positionCurrent < (deadBand + 1))
|| (positionTarget > (999 - deadBand) && positionCurrent > (999 - deadBand)))
{
// Stop the motor
output = 0;
positionError = 0;
}
// Else, update motor duty cycle with the newest output value
else
{
// This equation represents the control loop
output = (Kp * velocityError);
// Saturate the output at +/- 100 duty cycle,
if (output > 100)
output = 100;
else if (output < -100)
output = -100;
}
}
As you can see, this particular code sample estimates current velocity by taking the difference between the current position and the position 64 iterations ago and dividing by the time difference between the two positions. This is a very rough estimate, but is acceptable in this application because the actuators move relatively slowly and don't take long to reach their maximum speed. More complex applications may call for more accurate velocity estimates.
Target velocity is simply the difference between the current and target position, multiplied by a control gain so it can be tuned. Increasing Kv will result in a sharper deceleration when the actuator gets close to its target, but increasing it too much will cause it to overshoot and oscillate. Theoretically you'd also divide the difference by the change in time (dt), but since we're multiplying it by a gain that we have complete control over, this is unnecessary. The target velocity is then limited to the user-chosen maximum.
The termination condition of this control loop is the same as the PID position control- when the motor reaches its target position when the actuator is moving slowly enough, the loop will stop.
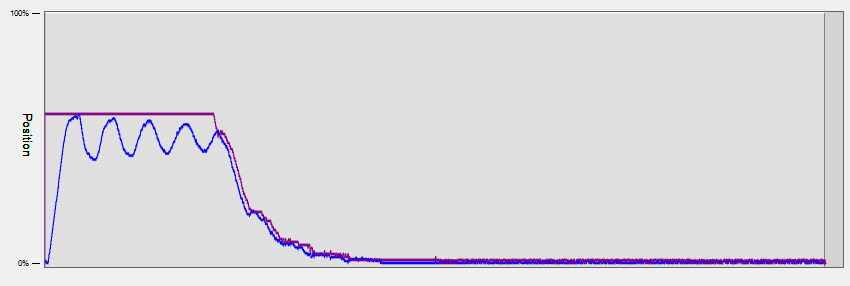
The violet line in the above plot represents target velocity, and the blue line is the estimated current velocity. As you can see, our purely proportional system isn't doing too well. We can tune the control gains to make it a little bit better, but we're probably better off adding more complexity to our control loop.
Integral Control
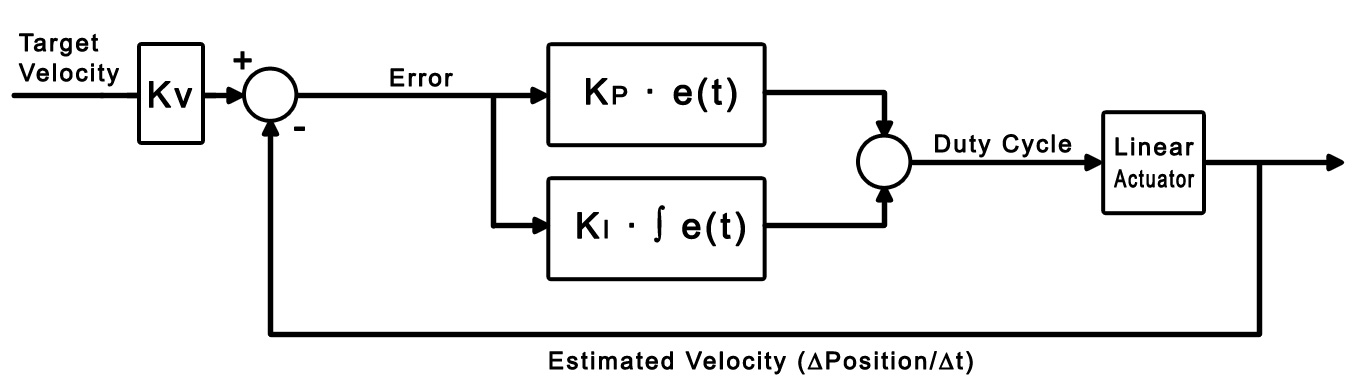
Just like the PID control system, we'll use an integral term to look at past error to influence current decisions. Here's what the control function would look like:
void ControlLoop()
{
// Update position array and variables
for (int i = 63; i > 0; i--)
{
positionArray[i] = positionArray[i-1];
}
positionArray[0] = positionCurrent;
positionOld = positionArray[63];
// Update velocity variables
velocityCurrent = (positionCurrent - positionOld) / (64 * dt);
velocityTarget = (positionTarget - positionCurrent) * Kv;
// Limit target velocity to the user-specified amount
if (velocityTarget >= maxOutput)
velocityTarget = maxOutput;
if (velocityTarget <= -maxOutput)
velocityTarget = -maxOutput;
// Update error values
velocityError = velocityTarget - velocityCurrent;
positionError = positionCurrent - positionTarget;
// If the error is within the specified deadband, and the motor is moving slowly enough
// Or if the motor's target is a physical limit and that limit is hit
// (within deadband margins),
if ((Math.Abs(positionError) <= deadBand && Math.Abs(output) < 5)
|| (positionTarget < (deadBand + 1) && positionCurrent < (deadBand + 1))
|| (positionTarget > (999 - deadBand) && positionCurrent > (999 - deadBand)))
{
// Stop the motor
output = 0;
positionError = 0;
}
// Else, update motor duty cycle with the newest output value
else
{
// This equation represents the control loop
// The first term is the velocity error multiplied by the proportional constant
// The second term is the feed-forward velocity estimate,
// and the third term is the accumulated integral times the integral constant.
output = (Kp * velocityError) + (Ki * integral);
// Saturate the output at +/- 100 duty cycle,
if (output > 100)
output = 100;
else if (output < -100)
output = -100;
// else, accumulate the integral
else
integral += (velocityError * dt);
}
}
The only difference in this version of the code is the accumulation of the velocity error, which is multiplied by a control gain and added to the output. See the integral section of the PID control application guide for more information on the integral term and how it works.
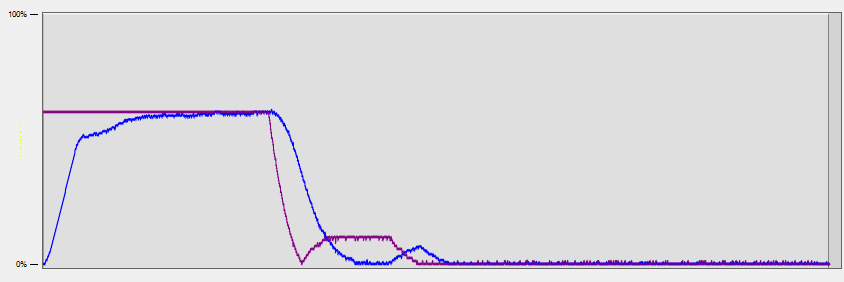
As before, the violet line is the target velocity and the blue line is the estimated actual velocity. This result looks much better than the purely proportional solution, but it oscillates a bit because it's taking a while to settle on the target position. Again, we can adjust the control gains to get a better response, but there's one more term we can add that will help with this control loop.
Feed-Forward Control
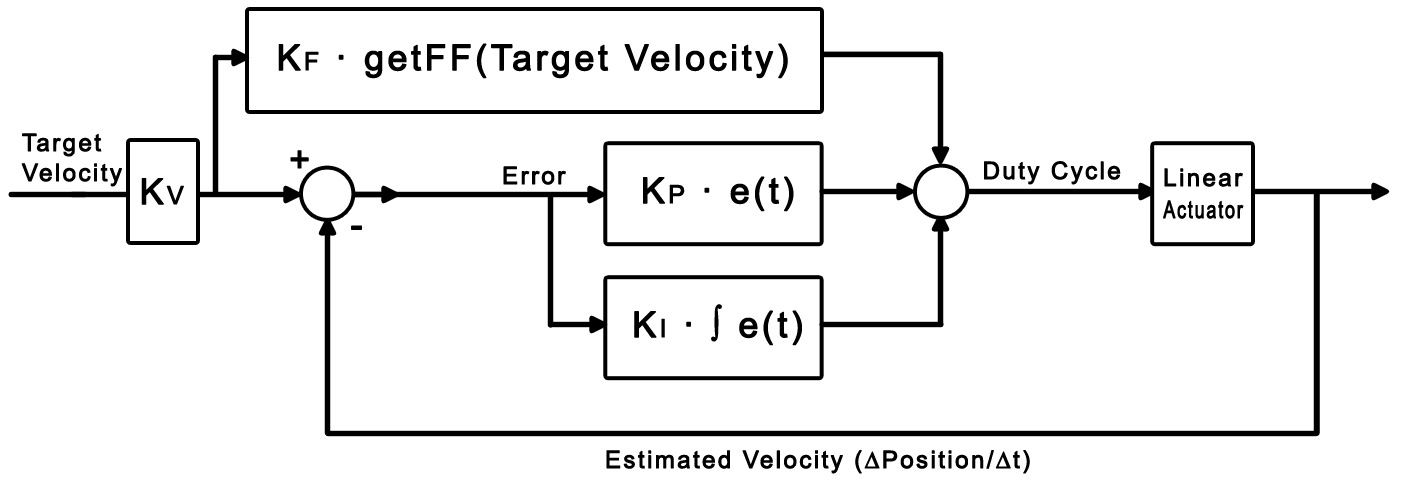
The concept behind feed-forward control is fairly simple: In a system where you're able to predict the behaviour
of the parts in that system, you can make estimates of what the output of the control loop should be,
and adjust accordingly. In this example, the linear actuator is the part that we'll be making predictions
on. The whole purpose of this control loop so far has been to control the velocity of the actuator (measured
in mm/second or SensorValue/second) by using a control loop whose output is in duty cycle (a percentage
of the motor controller's maximum power). Now, for any given actuator, if we can make the assumption
that it will repeatedly move at the same speed under the same conditions (load, power supply, etc), then
we can make a fairly accurate estimate for how much duty cycle results in a certain velocity in SensorValue/second.
We can feed this duty cycle into our control loop in order to reach our velocity target more accurately.
Our control loop function will look the same as in the previous section, except the output equation will
be changed:output = (Kp * velocityError) + (Kf * getFF(velocityTarget)) + (Ki * integral);
The function getFF() simply converts velocityTarget from SensorValue/second
to the estimated matching duty cycle using an array of pre-defined values and linear interpolation between
those values.
// FFarray is the array of expected motor velocities (units: sensorValue per second)
// that correspond with the duty cycle in increments of 20
double[] FFarray = new double[11] {-228, -182, -136, -91, -46, 0, 46, 91, 136, 182, 228};
// FFdutycycle is the array of duty cycles in increments of 20. This array is constant.
int[] FFdutycycle = new int[11] {-100,-80, -60,- 40,-20, 0,20, 40, 60, 80,100};
int getFF(double feedforward)
{
for (int i = 0; i < 10; i++)
{
// If feedforward is between two points on the characteristic curve,
if((feedforward >= FFarray[i]) && (feedforward <= FFarray[i+1]))
{
return (int)interpolate(FFarray[i], FFdutycycle[i], FFarray[i + 1], FFdutycycle[i + 1], feedforward);
}
}
// If feedforward is greater than the maximum value of the characteristic curve,
if (feedforward > FFarray[10])
return 100; // return the maximum duty cycle
// If feedforward is less than the minimum value of the characteristic curve,
else if (feedforward < FFarray[0])
return -100; // return the minimum duty cycle
// Else, something is wrong with the characteristic curve and the motor should be stopped
else
return 0;
}
If the user populates FFarray with velocity values measured while testing the actuator with the load that you intend to use with it, it should provide an accurate prediction (See the controls and settings section for more information). In applications where the load changes sporadically, this simple feed-forward will not be as useful.
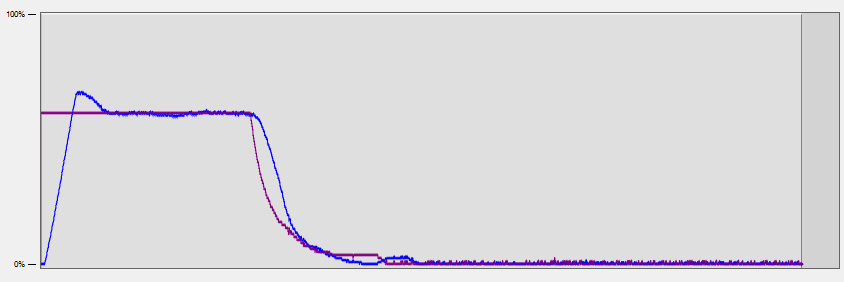
With proportional, integral, and feed-forward control implemented, the actuator reaches the target velocity much more reliably and doesn't oscillate around the target position.
Sample Program
You can download the sample program written for this guide. This is a Visual C# project.
Controls And Settings
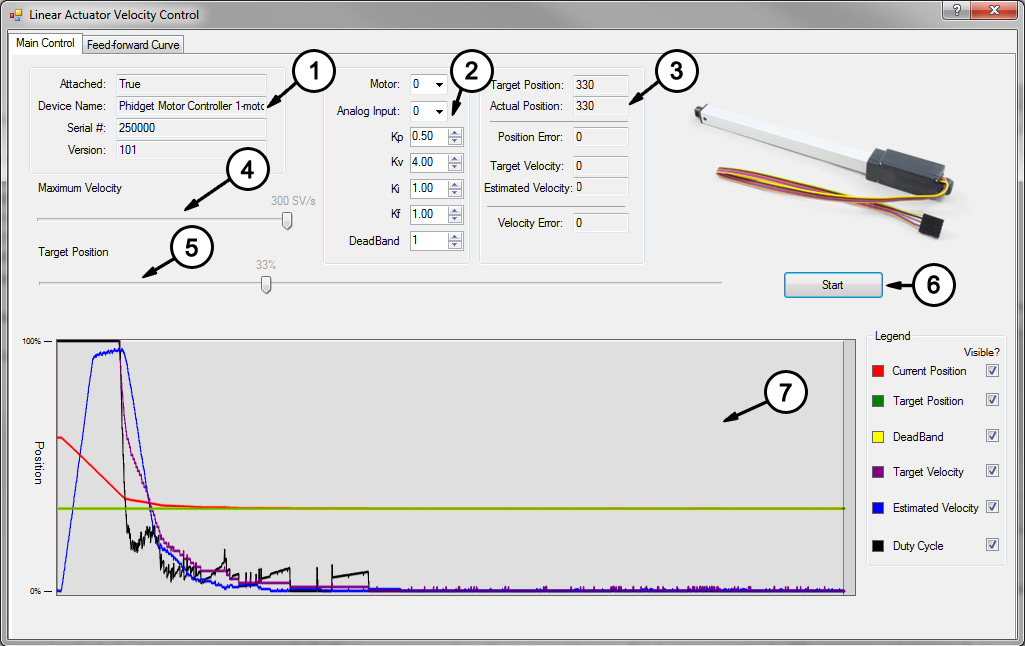
- These boxes contain the information of the attached motor controller. If these boxes are blank, it means the controller object didn't successfully attach.
- These boxes control which motor output and analog input are being used, and allow you to set each of the control gains. You can click on the "?" icon in the top right for more information on a particular setting. Changes will not take effect until the "Start" button is hit.
- These boxes display the target position set by the slider and the actual position according to the feedback potentiometer. The error is the difference between these two values, and the output velocity is the duty cycle of the controller as dictated by the control loop.
- The maximum velocity slider controls the target velocity for the control loop to aim for, in SensorValue per second. (For example, 100 SV/s would move one tenth of the actuator's full stroke length in a second, assuming the feedback potentiometer is a full 0-5V range)
- This slider selects the target position, from 0 to 100% of the actuator's full stroke length.
- Pressing the start button will initiate the control loop and the actuator will begin to move toward the target position, trying to move at the maximum velocity. If the actuator does not move, check your power and connections.
- This graph will plot the actuator's actual position, target position, estimated velocity, target velocity, and duty cycle over time. You can disable certain variables in the legend to make it easier to read.
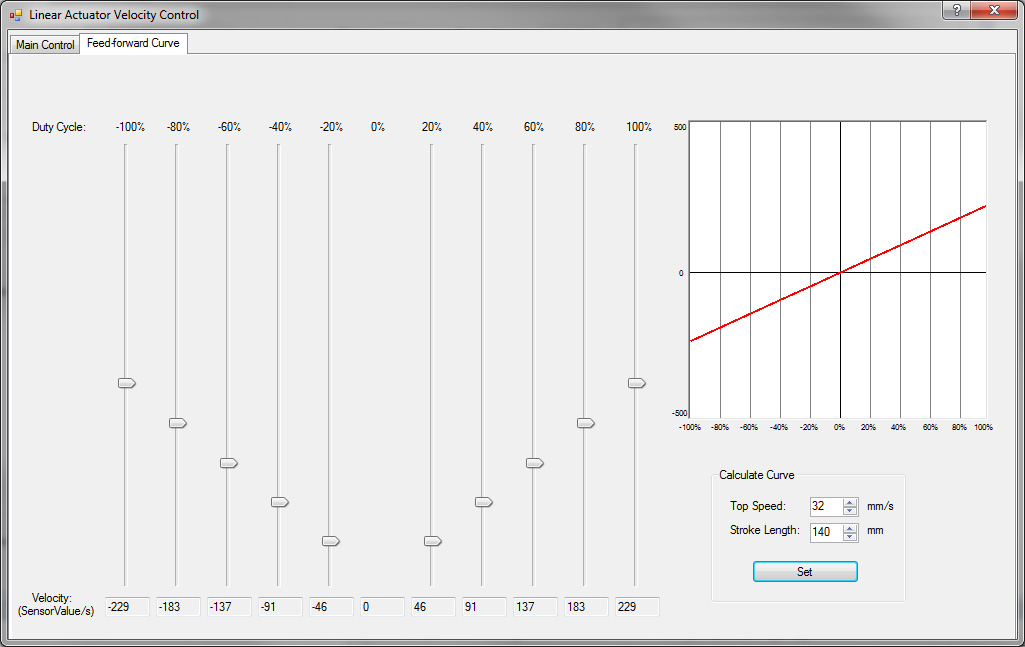
Click on the Feed-forward Curve tab at the top of the form to open the curve editor. You can adjust each slider to change the expected velocity of your actuator driving the intended load at various duty cycles. Alternatively, you can enter in the maximum speed and the stroke length of the actuator in order to automatically set the sliders to a linear estimate. The more accurate your estimates are, the more useful the feed forward term will be in the velocity control loop. Applications that involve intermittent and unpredictable loads will not have much use for this feature.
Algorithm
The algorithm in this program works the same way as the algorithm in the PID Control Application Guide, with the addition of the feed-forward term instead of the derivative term.
