|
Notice: This page contains information for the legacy Phidget21 Library. Phidget21 is out of support. Bugfixes may be considered on a case by case basis. Phidget21 does not support VINT Phidgets, or new USB Phidgets released after 2020. We maintain a selection of legacy devices for sale that are supported in Phidget21. We recommend that new projects be developed against the Phidget22 Library.
|
DC Motor and Controller Primer

|

|
Introduction
A DC motor is an electric motor that runs on DC current. They are commonly found in applications as diverse as industrial fans, blowers and pumps, machine tools, household appliances, power tools, disk drives, and many more.
Choosing a DC motor
There are 3 things to consider when choosing a DC motor.
- Current Consumption - You need to make sure that the controller you have is capable of providing enough current to drive your motor at its full rated current.
- Torque - Choose a motor that has enough torque to accomplish your goal.
- Speed - In the case of fans or RC cars you will need to choose a motor that can spin fast enough to be useful.
Note that while Phidgets sells several DC Motors, if your requirements are not met by any of them you can still use one of our DC Motor Controllers with a motor from a 3rd party. You just need to make sure that the motor's specs are less than or equal to what the motor controller is capable of driving. For example, the 1064 - PhidgetMotorControl HC has a continuous motor current of 14A, and takes a power supply of up to 15V DC. This means that the current ratings for your third-party motors should not add up to more than 14A, and each motor should be rated for no more than 15V DC if you want the advertised torque and speed of the motor.
For more information comparing DC motors with stepper motors and servo motors, see the Motor Selection Guide.
Types of DC motor
Brushed DC motors
Brushed DC Motors are very simple to understand, but very difficult to control precisely. By applying a voltage, or pulsing a voltage rapidly, at the terminals of the motor, current flows through the motor, and it will begin rotating. Depending on the direction of the current, the motor will rotate clockwise or counterclockwise. The brushes inside the motor automatically flip the direction of current inside the motor, allowing the motor to rotate continuously without the external precise control required for stepper motors. This is a huge benefit because it means the cost and complexity of controllers for this type of motor goes significantly down. There are two downsides of letting the motor ‘sequence’ itself.
- It’s not possible to control the timing - the motor will rotate as fast as possible, given it’s construction, the voltage applied, and the load it is driving.
- The brushes generate sparks and Electromagnetic Interference, and have a fairly limited lifetime.
Given that the speed of the DC motor depends on its construction, the load it is driving, and the voltage applied, the only practical way to change the speed of the motor is by changing the applied voltage. Typically this is done by changing the percentage of time the full supply voltage is applied to the motor. By switching the voltage very quickly (a technique called PWM or pulse width modulation), the controller is made smaller, more efficient, and cheaper.
Brushless DC motors
These motors require the motor controller to deliver AC power. This design is simpler than brushed motors because it eliminates the complication of transferring power from outside the motor to the spinning rotor. Brushless motors have longer life spans and are more efficient than their brushed counterparts, but they are significantly more expensive and require much more complex and expensive controllers to operate.
Uncommutated motors
Homopolar motors
A homopolar motor has a magnetic field along the axis of rotation and electric current flowing in a direction not parallel tot he magnetic field. Homopolar motors necessarily have a single-turn coil which means they are limited to very low voltages restricting its practical use.
Ball bearing motor
A ball bearing motor is an unusual electric motor that consists of two ball bearings with the inner races (surface) mounted on a common conductive shaft. The outer races (other side of the bearing) is connected to a high current source. This method has the advantage that the tube will act as a flywheel. The direction of rotation is determined by initial spin which is required to start the motor up. This type of motor is very uncommon.
Linear Actuators
A linear actuator is simply a DC motor that has been geared in such a way that it extends and retracts an arm instead of spinning a shaft. Depending on the power of the motor and the reduction ratios of the gearbox, linear actuators range from slow (0.5 inches/sec) to very fast (9 inches/s). Linear actuators are often specified for a certain "Load Capacity". This is analogous to a conventional motor's stall torque.
Linear actuators almost always come with built-in limit switches. These allow the motor to stop trying to extend or retract once it's near the limit. Without limit switches, a linear actuator could easily damage itself by trying to extend beyond its physical limit.
Some linear actuators come with a built-in potentiometer or rheostat, allowing it to know the approximate position of the arm. With this information, you could program a control system to actively control the position of the arm.
Achieving rough control of DC Motors
Depending on your application, you may not need precise control of the motor. If your power supply voltage and load are relatively constant, and you can tolerate some small variation in speed, simply tuning the Velocity in software to get the results you want will work. Using a DC Motor as a fan is a suitable example- Since the fan only needs to turn on and spin as fast as it can, it doesn't need any sort of control system. However, without the use of an encoder or some kind of feedback device, you won't be able to actively brake the motor or make it hold its position and resist rotation.
Achieving precise control of DC Motors
Encoder Input
The true acceleration, velocity and number of rotations of a DC motor is controlled by using an encoder to measure the movement of the motor shaft. The encoder rotates with the motor, and produces pulses. An encoder with very high resolution will produces thousands of precisely spaced pulses with a single rotation - an encoder with lower resolution will produce a dozen pulses. Please note we are referring to Quadrature (incremental) Encoders. By having electronics counting the number of pulses, and the time between pulses, it’s straightforward to calculate the velocity of the motor, and how far it has rotated. Use high CPR (counts per rotation) encoders (500 - 1000) for maximum precision.
An encoder is often placed on the exposed rear shaft of the motor. In this situation, remember to factor in the gearbox reduction ratio when calculating motor position and speed, since the rear shaft of a motor doesn't spin at the same speed as the gearbox output shaft.
Control Loops - Overview
A software control loop is an algorithm in your software application that receives sensor data, and uses that data to calculate how hard and in what direction it should drive the motor to achieve it’s goal. Control Theory is an extremely complex academic field, and in most cases there are simpler methods. If your application is simple - opening a door with two limit switches, for instance, no fancy algorithm is required.
PID Loop
To control a motor’s position and/or velocity under varying load conditions - a common application - the PID loop is a place to start. The performance of the system is determined by tuning three parameters for the Proportional, Integral and Derivative terms. If you are familiar with Control Theory, these parameters can be calculated accurately. For the rest of us, the typical approach is to first tune the Proportional Term, increase the Integral term if necessary, and usually leave the Derivative term at zero. At its most basic a PID controller looks like this:
where
- : Proportional gain, a tuning parameter
- : Integral gain, a tuning parameter
- : Derivative gain, a tuning parameter
- : Error, or the difference between the current value and the target value
- : Time or instantaneous time (the present)
The proportional term sets how strongly the system responds immediately to the difference between it’s target goal, and it’s current measured performance. For example, if the cruise control on a car is set to 100 kph, and the speedometer indicates the speed is 90 kph, the proportional term sets how much throttle is applied.
The integral term allows the control loop to respondly more strongly over time to situations where the proportional term is unable to reach the target. The integral term can be thought of as a slowly building impatience within the control loop.
The derivative term is used to prevent the control loop from overshooting the target. In practice, it requires very precise measurements to calculate how quickly the loop is approaching the target. In many systems, the measurements are not accurate enough, and the derivative term only causes system instability.
| Parameter | Rise time | Overshoot | Settling time | Steady-state error | Stability |
|---|---|---|---|---|---|
| Decrease | Increase | Small change | Decrease | Degrade | |
| Decrease | Increase | Increase | Decrease significantly | Degrade | |
| Minor decrease | Minor decrease | Minor decrease | No effect in theory | Improve if small |
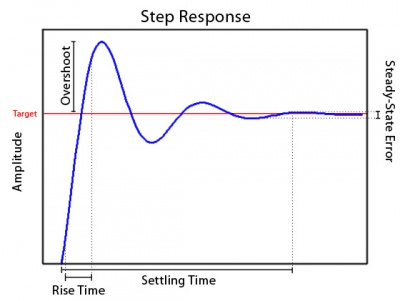
Where:
- Rise time is the time it takes for the system to go from rest to within a certain percentage of its target value. This is usually measured as the 10-90 rise time or the time it takes to go from 10% of the way to the target value to 90% of the way to the target.
- Overshoot is how far the system overshoots its target value before turning around to come back like a spring (this can be 0 in some systems).
- Settling time is how long it takes for the oscillations in the system to get below a certain amount. Typically this is measured as the 2% or 5% settling time meaning the time for the oscillations to get within 2 or 5% respectively of the target value.
- Steady-state error is the distance from the target once the oscillations have reached a constant state. This is usually a small number and for most practical systems can be entirely ignored if the controls have been well chosen. If the parameters are made too large, the steady-state error will become infinite meaning the system has become unstable and will vibrate around the target wildly.
- A system is considered stable if the steady-state error is finite.
Sample Code
Here is some code for a simple PI loop. The term has been left out because it is very difficult to correctly tune and often just leads to instability in the system. For a more in depth look you can also look at our PID loop example here.
Kp = ? //proportional control
Ki = ? //integral control
Ko = ? //overall gain
MAXOUTPUT = ? //max output wanted by the motor
DEADBAND = ? //allowable region of error around target
dt = feedbackPeriod;
feedback = sensor.Value;
error = target - feedback;
//Create a dual-sided deadband around the desired value to prevent noisey feedback from producing control jitters
//This is disabled by setting the deadband values both to zero
if (Math.Abs(error) <= DEADBAND)
{
error = 0;
if (target == 0)
output = 0;
}
else
output = ((Kp * error) + (Ki * integral))/Ko;
//Prevent output value from exceeding maximum output, otherwise accumulate the integral
if (output >= MAXOUTPUT)
output = MAXOUTPUT;
else if (output <= -MAXOUTPUT)
output = -MAXOUTPUT;
else
integral = integral + (error * dt);
errorLast = error;
motoControl.motors[0].Velocity = Math.Round(output);
Kalman Filter
More sophisticated control loops, like Kalman filters, are built with specialized knowledge of the exact application. In fact, a Kalman filter is not so much a filter as it is a mathematical model of the application, incorporating the laws of physics, and expectations of how the system should behave and respond. With the cruise control example, if the wheels spin on black ice, the PID loop will not respond appropriately. An experienced driver, and a much more sophisticated control algorithm like a Kalman filter will realize that something unusual is happening.
For more information on Kalman filters check out this link: http://en.wikipedia.org/wiki/Kalman_filter Warning: if you are not very familiar with state space equations and advanced control theory this will not help you much.
Impact of Latency on Control Loops
There is a time delay required to measure the system (encoders, Back EMF, current, sensors, etc.), receive this data in your application, and send the new target velocity to the Motor Controller. If the system being controlled by the control loop can respond as quickly, or quicker than this time delay, the system will be plagued by oscillations.
Gearboxes
A gearbox is a motor attachment that uses the mechanical advantage of gears to either increase torque at the cost of speed, or increase speed at the cost of torque. Often times, motors are faster than necessary for their application, but lack the required torque. A gearbox can be used to take the excess speed and convert it into extra torque. For example, if a motor had a gearbox with a 5:1 reduction ratio, it would mean that the output shaft of the gearbox will rotate once every five times the motor's shaft rotates. This means that the shaft will rotate five times slower than if it didn't have the gearbox, but it will have five times the torque (minus a bit, since some energy will be lost to friction and heat inside the gearbox). By reducing the speed of the shaft, you also increase its precision. For example, if your motor controller can control the velocity of your motor with a resolution of 1.5% of the motor's maximum velocity, then a 5:1 reduction ratio would allow you to control the output shaft with a resolution of 0.3% of the motor's maximum velocity.
In order to achieve high reduction ratios, you need a large number of teeth on the output gear. Since most gearboxes are too small to house a single gear with many teeth, a gearbox will often contain several "stages", where each stage has its own set of gears. Each successive stage reduces the gear ratio a bit more. However, a larger number of stages usually results in more power lost to heat and friction inside the gearbox.
Types of Gearboxes
Spur Gearboxes
A spur gearbox is one of the simplest types of gearboxes. It is designed simply to provide a specific reduction ratio. Because of its simplicity, a spur gearbox is typically inexpensive. Spur gearboxes will typically be rated for lower torque than other types of gearboxes of the same size, because all of the torque is focused on one gear junction.
Planetary Gearboxes
A planetary gearbox has a more complex gear layout that allows torque to be loaded evenly across multiple planetary gears. They are more expensive, since they contain more gears per stage, but they are also more efficient and have less backlash. Planetary gearboxes are typically rated for higher speed also, since the design is better suited to recirculating oil throughout the gears. A planetary gearbox will often be noisier than a spur gearbox of the same quality, because there are more points of contact inside the gearbox.
Maximum Strength of Gears
Often a gearbox will be rated for a certain amount of torque. This value is the absolute maximum torque that the gearbox should have to endure. You can probably run it above this value, but doing so will drastically shorten the lifespan of the gearbox. If you have a powerful motor that is able to produce more torque than your gearbox is rated for, you must control the motor carefully to ensure that you don't damage the gearbox. Even if your motor is incapable of producing such a large amount of torque by itself, the load it's driving could resist hard enough to damage the gearbox.
Axial Load and Radial Load
Axial Load
- The axial load of a gearbox refers to the maximum force the gearbox can endure in a direction parallel to the output shaft. Exceeding this value will reduce the gearbox efficiency and shorten the lifespan. For example, if the motor was being used to turn a miniature carousel from underneath, the weight of the carousel pushing down on the motor's shaft would contribute to the axial load. This type of force often arises from sudden physical impacts to the axle the motor is driving. These types of forces can be mitigated with the use of external bearings.
Radial Load
- The radial load of a gearbox refers to the maximum force the gearbox can endure in a direction perpendicular to the output shaft. Exceeding this value will reduce the gearbox efficiency and shorten the lifespan. For example, if the motor is being used to turn a pulley, the tension on that pulley would contribute to the radial load on the motor's shaft. This type of force is most often encountered when trying to use a motor to drive an axle directly. Keep in mind that the longer the axle is, the more leverage the radial force will have on the motor's shaft. Even if the motor is mounted close to a tire, if the tire is wide it will still have considerable leverage on the motor's shaft. In applications with high potential for radial load, it would be advisable to drive the axle indirectly.
Torque, Speed, Voltage and Current
Constant Voltage
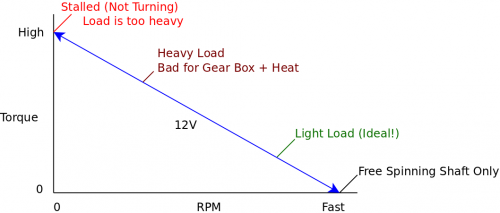
In a simple example with no motor controller, when you constantly provide the rated voltage (12V in this example), the motor will try to spin as fast as it can based on the magnitude of the load resisting it.
The blue line in the above graph illustrates the range of torque/speed values that the motor could operate at depending on the magnitude of the load.
At the far left, the load is too heavy; the motor will try to apply the needed force and fail, resulting in zero speed. This is called stalling. When stalling, the motor is pushed to its limit, causing it to consume the maximum possible amount of current for this particular supply voltage (This value is known as "Stall Current"). Since the motor is consuming the highest possible electrical power, it also outputs the highest possible mechanical power ("Stall Torque") while stalling. It is not a good idea to stall a motor, because it will very quickly overheat from the increase current draw and eventually burn out. When using a motor controller, the board will often have a maximum current rating based on the board's ability to dissipate heat. You could add heatsinks, fans, or other cooling devices to the board to increase the current limit, but do so with caution. Unless you have a way of monitoring the temperature of the driver chip during operation, you have no way of knowing how far beyond the rated specification you can go.
At the far right, the motor shaft is spinning freely, with no load other than the force required to spin the shaft. The motor will keep spinning faster and faster, until the back EMF generated by the motion of the motor reduces the current and limits the speed to a maximum value.
Since torque and RPM are linearly related, these two extreme cases represent points that create a line along which the motor can operate. Reducing load (and therefore the required torque) increases speed, and vice-versa. When voltage is held constant, the motor can only operate along this line, which is inconvenient when you want to vary speed at a constant load (for example, speeding up or slowing down a remote-controlled car).
Dynamic Voltage
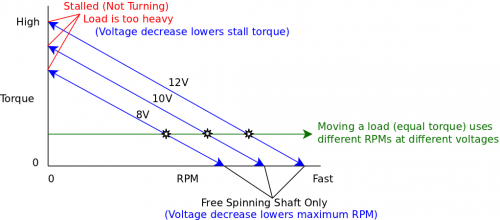
Building on the previous example, lets say that we're using a motor controller that enables switching between three voltage levels: 8V, 10V and 12V. Please note that while it's acceptable to provide less than the rated voltage, you should not supply a motor with significantly more than the rated voltage. In this example, assume the motor is rated for 12V.
When you change the voltage, the relationship between RPM and torque changes. A lower voltage produces a second line parallel to the first, with a lower stall torque and free-spinning RPM, for the motor to operate across.
At a constant load, decreasing the voltage means decreasing the speed, as illustrated by the three black points on the green line.
Pulse-Width Modulation
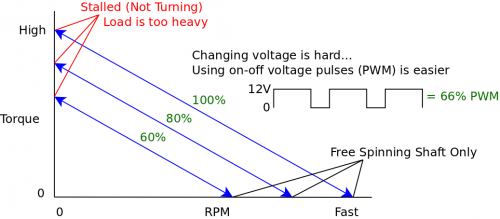
Now, constantly changing the amount of DC voltage supplied to the motor is difficult without expensive hardware and large efficiency losses.
The most effective solution to this problem is called pulse-width modulation (PWM for short).
PWM involves giving the motor an AC signal that varies from zero volts to the full amount (12V in this example). For each period of the PWM waveform, the value is high for a certain percentage of time. This percentage is called the duty cycle. For example, a waveform that is high (12V) for two thirds of each period and low (0V) for one third of each period would have a 66% duty cycle, as shown in the waveform in the diagram.
Normally you might expect these sudden pulses of power to result in stuttering or jerky movements in the device being powered. However, since motors are essentially large coils of wire, they act as inductors which have a smoothing effect on this signal. Thus, by providing a 12V PWM signal at a 50% duty cycle, you can simulate the effect of using a 6V power supply. It is very easy and inexpensive to implement PWM, and you can choose virtually any duty cycle (limited by how precisely the controller can generate the PWM waveform), which means the motor could be operated at any point on the graph below the 100% line.
Peak Efficiency
Key concepts:
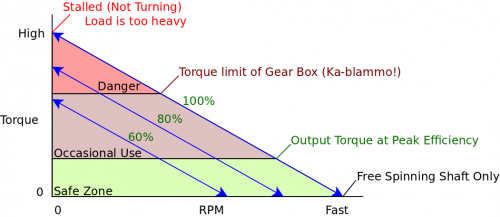
The above graph is separated into three sections based on the size of the load that the motor is working against (and consequently the amount of torque being applied).
The green zone indicates the range of torque values where the motor is running at peak efficiency. This zone starts at the rated torque for the motor, and continues down to the maximum speed (free spinning shaft) point. When in this zone, the motor has the highest efficiency (conversion of electrical to physical power), and will draw current equal to the rated current value, assuming the motor is also running at the rated voltage. In order to maximize the lifespan of your motor, you should choose a motor that has a high enough rated torque that your application runs in this zone most of the time.
The brown zone indicates the range of torque values where the motor is running at reduced efficiency. This zone starts at the physical limit of the motor and continues down to the rated torque. If the motor has a gearbox, the upper limit of this zone is usually the torque limit of the gearbox. The motor can be operated in this zone occasionally, for short periods of time. If the motor is run in this zone constantly, it will reduce the lifespan of the motor significantly. You may be familiar with the "burned" smell of a DC motor that's running too hard and overheating- this is not from high speed, but from low speed and high torque.
The red zone indicates the range of torque values where the motor is stalling or nearly stalling. This zone starts at the stall torque for the motor, and continues down to the physical limit. If the motor has a gearbox, operating in this range will cause extreme wear on the gears, and the gearbox will eventually seize if left in this zone too long. Running a motor in this zone will drastically reduce its lifespan due to overheating.
Comparing Motors
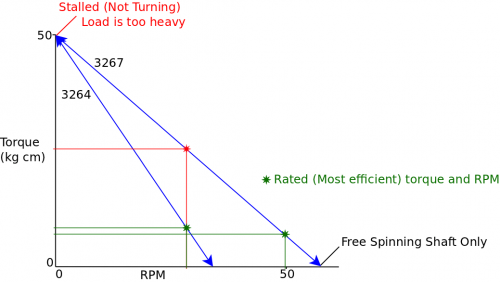
In the above graph, we compare two DC motors: the 3264 and the 3267. Both motors have approximately the same stall torque, as seen by the intersection of the blue lines at the top of the graph. Both motors have a similar rated torque also, but the 3267 has a much higher rated RPM (as shown by the green lines).
From looking at the motor specifications, you might simply think of the 3267 as a motor with the same torque as the 3264, but with more RPM. This is true, but you could also think of it this way: The 3267 could be run at the rated RPM of the 3264, but at a much higher torque (as evidenced by the red lines). Keep in mind, however, that this would cause the 3267 to run outside of its peak efficiency zone. The important thing to take away from this graph is that torque and speed go hand-in-hand, and you don't really get the full picture by simply comparing stall torques, rated torques or rated RPM values.
Example: Two-motor Vehicle Control
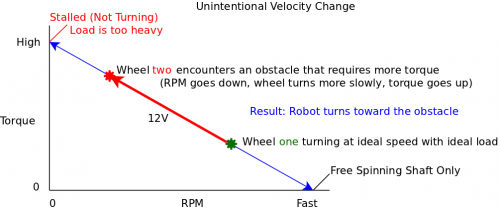
In this example, we will illustrate how PWM control can aid in navigation for a two-motor robot (each motor drives one side of the vehicle).
The above graph illustrates a major weakness of using a DC motor in an application with unpredictable, inconsistent torque requirements.
Imagine our vehicle is driving in a straight line on level terrain. The motor controller is telling the motors to go at a specific speed (through PWM), and the vehicle doesn't have any problems with this. But when one of the wheels encounters some difficult terrain (bumpy, slippery, etc), that wheel is forced to operate at a higher torque value along the blue line, which results in lower speed. When the wheels on one side of a vehicle rotate more slowly than the wheels on the other side, it causes the vehicle to turn in the direction of the slower wheel.
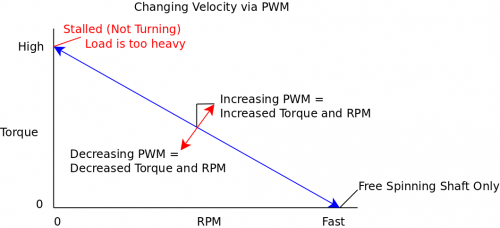
Now, in a scenario with a constant torque value, the motor controller can only change the PWM duty cycle. By increasing the duty cycle, you increase both the torque and the RPM (as shown by the black line vector components). In this case we cannot change RPM and torque individually.
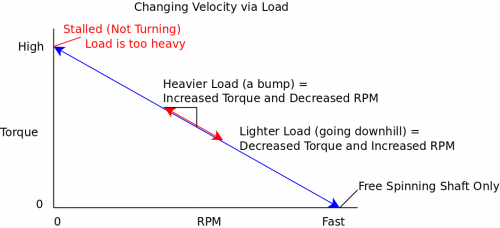
In this case, the PWM duty cycle is held constant, but the load is changed (in this example, because of difficult terrain). When this happens, both RPM and torque change, and we're unable to change torque or RPM individually to compensate and keep moving at a constant speed. If we combine the concepts of these previous two graphs, we can devise a method to control the RPM for a changing load.
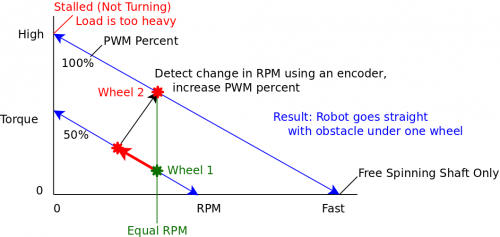
In this solution, we attach encoders to each wheel so we can tell when it has encountered an obstacle that is decreasing its speed (red line in the graph). When the speed decrease is detected, the motor controller bumps up the PWM duty cycle of that motor by an amount that will result in both wheels having the same RPM (green line in the graph). When the wheel passes the obstacle, the reduction in the load will cause the speed to increase, and the motor controller will detect this increase and bring the PWM duty cycle back down to normal. In order for this solution to work, the motors need to operate at a lower default PWM duty cycle so that increasing the duty cycle to bypass difficult terrain is an option.
Wire Length
Since the DC motor controller is sending a fairly simple signal to the motor, interference from having long wires is not a big concern. You should be able to have quite long wires between your motor and controller. For more information, see the effects of long wires page.








