|
Notice: This page contains information for the legacy Phidget21 Library. Phidget21 is out of support. Bugfixes may be considered on a case by case basis. Phidget21 does not support VINT Phidgets, or new USB Phidgets released after 2020. We maintain a selection of legacy devices for sale that are supported in Phidget21. We recommend that new projects be developed against the Phidget22 Library.
|
Compass Primer
Introduction
A compass is a navigational instrument that is used to determine direction relative to the surface of the earth. Compasses measure direction with respect to the 4 cardinal directions (North, East, South, West) with 0 degrees indicating straight North and 180 degrees indicating straight South.
Electronic compasses work in exactly the same way as any other compass: They detect the Earth's magnetic field and respond to it. The difference is that an electronic compass uses a magnetometer to detect the field as opposed to a small magnet. This allows them to be much more accurate and allows them to respond more quickly to changes in direction than a traditional compass ever could.
How Compasses Work
Small compasses found in clocks, mobile phones, and other electronic devices are solid-state compasses, usually built out of two or three magnetic field sensors that provide data for a microprocessor. The correct heading relative to the compass is calculated using trigonometry. Often, the device is a discrete component which outputs either a digital or analog signal proportional to its orientation. This signal is interpreted by a controller or microprocessor and used either internally, or sent to a display unit. The sensor uses highly calibrated internal electronics to measure the response of the device to the Earth's magnetic field.
Basic Use
Compasses are typically mounted on an object that the user wants to monitor the direction of. In order to get the most accurate readings it is recommended to mount the compass to the object in such a way that there is minimal room for shifting. You will need to calibrate the compass as well.
Calibration
Calibration involves setting the compass up to handle the magnetic field characteristics in your particular region of the world as well as disturbances caused by a more localized magnetic fields such as speaker magnets. To calibrate effectively you will need to determine the Earth's magnetic field strength at your location. This data is available on line in the form of magnetic field calculators all you have to do is enter in your zip or postal code.
Calibration is required for any applications needing more accuracy than a simple North, East, South, or West. If you have already gathered compass data, you can retroactively calibrate that data by applying the same calibration formula to each data point. You can find these formulae by looking at the source code of phidgetspatial.c in the Linux source code.
For more information on calibrating the compass on the 1056 refer to our calibration guide. The newer, 1042 and 1044s also require calibration and you can find a guide for calibrating them in their respective User Guides.
Interference
The most common problem compass users can expect to face is interference. Interference will generally cause the compass to behave poorly. Usually this means inconsistent, fluctuating, or inaccurate readings. Luckily most forms of interference are fairly easy to deal with.
What are likely sources of interference and how are they handled?
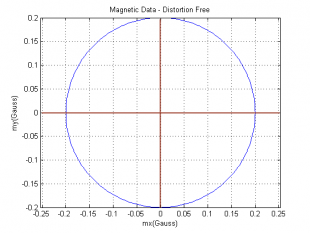
There are 4 main categories of interference. Some are easy to get rid of via calibration, others are not easy or even impossible to get rid of.
If you rotate the compass through a full 360 degrees and plot the resulting data on an x-y plane you will get a circle centered at the origin. This can be extended to a 3 axis compass which would generate a sphere. However, certain characteristics of the vehicle and environment can have a distorting effect on this magnetic data often in combination with one another to create significant interference. In fact the magnitude of the interference is regularly many times the that of the actual signal.
"Hard Iron" Interference
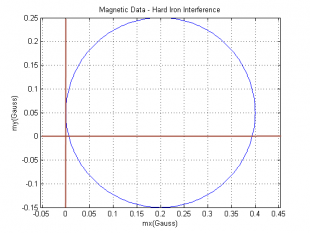
So called hard iron interference is caused by static magnetic fields associated with the vehicle. This can include any minor (or major) magnetism in the metal chassis or frame of the vehicle, any actual magnets attached such as speakers etc... This interference pattern is unique to the vehicle but is constant. If you have your compass in an enclosure that is held together with metal screws even these relatively small amounts of ferromagnetic material can cause issues. If we consider the magnetic data circle, hard iron interference has the effect of x/y(/z in the case of 3 axes) shifting the entire circle away from the origin by some amount. The amount is dependent on any number of different factors and can be very large. The important part is that this shift is the same for all points in time so it can be calibrated out very easily with a numeric offset which is taken care of by the calibration process.
"Soft Iron" Interference
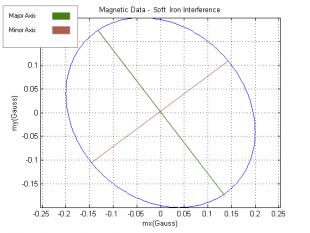
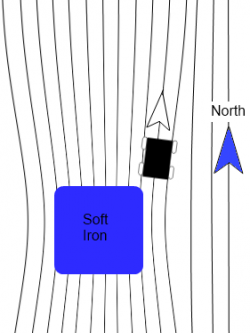
Soft iron interference is caused by distortion of the Earth's magnetic field due to materials in the vehicle's construction. Think of it like electricity, the magnetic field is looking for the easiest path to get to where it is going. Since magnetic fields can flow more easily through ferromagnetic materials than air, more of the field will flow through the ferromagnetic material than you would expect if it were just air. This distortion effect causes the magnetic field lines to be bent sometimes quite a bit. Note that unlike hard iron interference which is the result of materials which actually have a magnetic field of their own, soft iron interference is caused by non-magnetic materials distorting the Earth's magnetic field. This type of interference has a squishing effect on the magnetic data circle turning it into more of an ellipsoid shape. The distortion in this case depends on the direction that the compass is facing. Because of this the distortion cannot be calibrated out with a simple offset, more complicated math will still let the compass account for this type of interference though.
Dynamic magnetic fields associated with application
Most robots and vehicles have all manner of devices running on them other than just the compass. The wiring associated with these devices will create its own, dynamic magnetic field. Particularly bad offenders are electric motors that are running. The magnetic fields of these devices are constantly changing and calibration will only provide small (if any) benefits. The best thing that can be done to avoid this sort of interference is to mount the compass as far away from other electronics as possible.
Static or Dynamic fields not associated with application
These are the most difficult to handle. A very common cause of this sort of interference is steel or iron re-bar in concrete floors. Steel studs in office or commercial buildings are also a problem. In general any environmental (i.e. external) sources of hard or soft iron distortion can cause issues as the vehicle moves about. There is no practical way to account for this. The best thing you can do is to take a simple handheld compass and move it around in the area you intend the electronic compass to be operating. Does the compass report reasonable directions? If so then your system will likely function well. If not, the area is simply too noisy to use an electronic compass.
Combinations
In practical applications most of these types of interference work in combination. Because of all of this, to use a compass calibration is required.
Declination
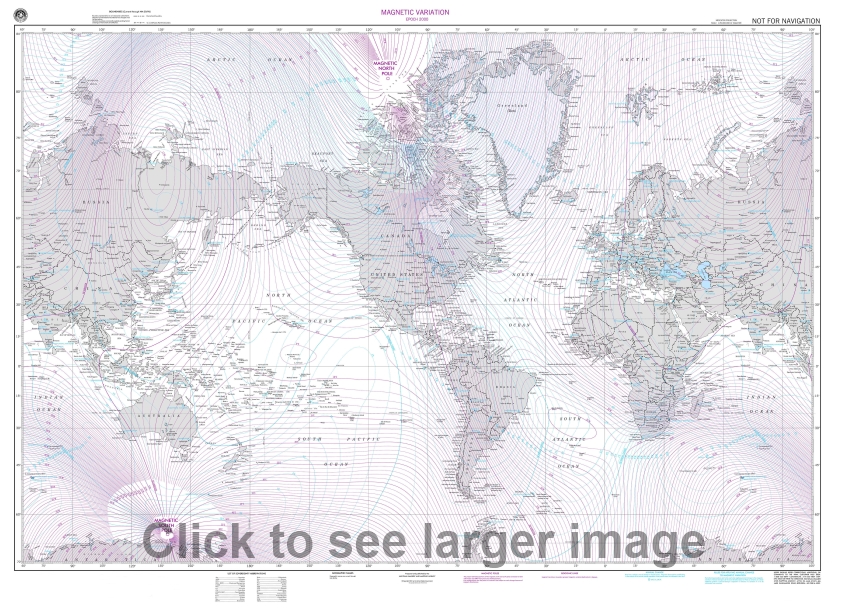
Over long periods of time changes in the Earth's magnetic core have an effect on the Earth's magnetic field. What this means is that the North Magnetic Pole shifts and is not the same as "true" North. The time it takes for magnetic North to shift significantly is very long so for all intents and purposes the magnetic North pole is stationary, it is just important to note that it is not in the same place as the actual North pole. Since compasses measure direction as a function of magnetic field strength, the direction a compass tells you is North is in fact magnetic North. As you might imagine the amount that magnetic North and true North differ is a function of your location. It is technically possible for your compass to point in the exact opposite direction from North if you are directly between the North pole and the magnetic North pole. The most common way to get declination is from a map that has isogonic lines. Isogonic lines are lines of equal declination similar to contour lines on topographic maps that show elevation. The lines will give a reasonable approximation of the declination for your region. For example, take a look at the map below and try to determine what the declination is in your city:
For the purposes of calculation assume that East declination is positive and West is negative. This means that you need to subtract the declination from your heading when your declination is to the East and vice versa when it is West.
Noise
As with all electronics, electronic compasses will be effected by some amount of noise, usually caused by thermal and mechanical fluctuations inside the sensor. Noise levels will be different for each axis, because each orientation of sensor is build slightly differently (for example, it is much more difficult to get low noise from the vertical axis because the sensor is a flat piece of silicon. Two of the major types of noise are white noise and random walk.
White Noise
White noise is the short-term noise that is contributed to from a number of internal and external factors. For example, when a compass is stationary on your desk, it might read 100μG one sample, 101μG another sample, and 97μG in yet another sample. Luckily, white noise is usually fairly consistent which means it can be mitigated quite effectively if you average multiple samples together. With a Phidgets Inc. compass, if you select a data rate slower than its maximum it will automatically average as many samples as it can within that time frame for each value. In applications where you need an extremely fast sampling rate, and can't afford to spend time averaging samples, you should look for a compass with low white noise. Also keep in mind the noisiness of your environment- For example, the engine and road noise on a bus will easily be more noisy than the compass - so there is no point in paying for a low noise device. See the Allan Deviation Primer for more information on spatial noise characteristics.
Random Walk
Often called drift, random walk is the long-term noise that causes samples to gradually become further and further away from their true values. This type of noise is less important for applications with constant movement and a fast sampling rate, but for applications where values are averaged over longer periods of time, it can cause severe inaccuracies. See the Allan Deviation Primer for more information on accelerometer noise characteristics.
Calculating Heading from Magnetometer Data
The three axis magnetometer data can be used, along with pitch and roll angles calculated from the accelerometer, to find a magnetic bearing - ie. as a compass. In order for the compass to be accurate at all, calibration must have been done to factor out hard and soft iron offsets.
The magnetic field is represented as a vector. If the spatial is completely level with respect to gravity, then we can calculate magnetic bearing easily by looking at the x and y components of the vector, which simply represents an angle between 0 and 360 degrees on the unit circle.
However, when the board is not level, the magnetic field vector components in each axis will be skewed, or is other words, what we need to know is the magnetic field with respect to the earth frame, and what we have is the magnetic field with respect to the 1056, which is rotated with respect to the earth. What needs to be done is to rotate the magnetic field vector back into the earth frame, we can then use the x-y components to again determine bearing. The easiest way to do this is to find the board pitch and roll angles using the accelerometer, and then build a rotation matrix using these angles to rotate the magnetic field vector into the earth frame (ie aligned with gravity). For example, here is an excerpt from our C# example code which shows how this is done:
//This finds a magnetic north bearing, correcting for board tilt and roll as measured by the accelerometer
//This doesn't account for dynamic acceleration - ie accelerations other then gravity will throw off the calculation
//Calculations based on AN4248
double[] lastAngles = { 0, 0, 0 };
void calculateCompassBearing()
{
double[] gravity = {
spatial.accelerometerAxes[0].Acceleration,
spatial.accelerometerAxes[1].Acceleration,
spatial.accelerometerAxes[2].Acceleration};
double[] magField = {
spatial.compassAxes[0].MagneticField,
spatial.compassAxes[1].MagneticField,
spatial.compassAxes[2].MagneticField};
//Roll Angle - about axis 0
// tan(roll angle) = gy/gz
// Use Atan2 so we have an output os (-180 - 180) degrees
double rollAngle = Math.Atan2(gravity[1], gravity[2]);
//Pitch Angle - about axis 1
// tan(pitch angle) = -gx / ((gy * sin(roll angle)) + (gz * cos(roll angle)))
// Pitch angle range is (-90 - 90) degrees
double pitchAngle = Math.Atan(
-gravity[0] / ((gravity[1] * Math.Sin(rollAngle)) + (gravity[2] * Math.Cos(rollAngle)))
);
//Yaw Angle - about axis 2
// tan(yaw angle) = (mz * sin(roll) – my * cos(roll)) /
// (mx * cos(pitch) + my * sin(pitch) * sin(roll) + mz * sin(pitch) * cos(roll))
// Use Atan2 to get our range in (-180 - 180)
//
// Yaw angle == 0 degrees when axis 0 is pointing at magnetic north
double yawAngle = Math.Atan2(
(magField[2] * Math.Sin(rollAngle))
- (magField[1] * Math.Cos(rollAngle))
,
(magField[0] * Math.Cos(pitchAngle))
+ (magField[1] * Math.Sin(pitchAngle) * Math.Sin(rollAngle))
+ (magField[2] * Math.Sin(pitchAngle) * Math.Cos(rollAngle))
);
double[] angles = {rollAngle, pitchAngle, yawAngle};
//we low-pass filter the angle data so that it looks nicer on-screen
try
{
//make sure the filter buffer doesn't have values passing the -180<->180 mark
//Only for Roll and Yaw - Pitch will never have a sudden switch like that
for(int i=0;i<3;i+=2)
{
if (Math.Abs(angles[i] - lastAngles[i]) > 3)
foreach (double[] stuff in compassBearingFilter)
if (angles[i] > lastAngles[i])
stuff[i] += 360 * Math.PI / 180.0;
else
stuff[i] -= 360 * Math.PI / 180.0;
}
lastAngles = (double[])angles.Clone();
compassBearingFilter.Add((double[])angles.Clone());
if (compassBearingFilter.Count > compassBearingFilterSize)
compassBearingFilter.RemoveAt(0);
yawAngle = pitchAngle = rollAngle = 0;
foreach (double[] stuff in compassBearingFilter)
{
rollAngle += stuff[0];
pitchAngle += stuff[1];
yawAngle += stuff[2];
}
yawAngle /= compassBearingFilter.Count;
pitchAngle /= compassBearingFilter.Count;
rollAngle /= compassBearingFilter.Count;
//Convert radians to degrees for display
compassBearing = yawAngle * (180.0 / Math.PI);
bearingTxt.Text = compassBearing.ToString("F1") + "°";
pitchAngleTxt.Text = (pitchAngle * (180.0 / Math.PI)).ToString("F1") + "°";
rollAngleTxt.Text = (rollAngle * (180.0 / Math.PI)).ToString("F1") + "°";
}
catch { }
}