1044 User Guide: Difference between revisions
No edit summary |
|||
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
__NOINDEX__ | |||
<metadesc>The PhidgetSpatial 3/3/3 Precision has a 3-axis accelerometer, gyroscope and compass with high resolution readings at low magnitudes.</metadesc> | |||
[[Category:UserGuide]] | [[Category:UserGuide]] | ||
==Getting Started== | ==Getting Started== | ||
{{UGIntro|1044}} | |||
*[{{SERVER}}/products.php?product_id=1044 1044 Spatial Phidget] | |||
*USB cable and computer | |||
Next, you will need to connect the pieces: | |||
[[Image:1056_0_Connecting_The_Hardware.jpg|500px|right|link=]] | |||
# Connect your device to your computer using the USB cable. | |||
[[ | |||
= | <br clear="all"> | ||
{{UGIntroDone|1044}} | |||
{{ | |||
== | ==Using the 1044== | ||
{{ | {{UGcontrolpanel|1044}} | ||
{{ | {{ugAccelerometer|1044|}} | ||
}} | |||
{{ugGyroscope|1044}} | |||
{{ | {{ugMagnetometer|1044}} | ||
{{ugSpatial|1044}} | |||
{{ | {{ugAddressingInformation}} | ||
{{ugUsingYourOwnProgram|1044}} | |||
{{ | |||
==Technical Details== | ==Technical Details== | ||
=== | ===Using Quarternion Algorithms=== | ||
====What is Quarternion?==== | |||
For the 1044_1, we have added support for quarternions which can be used instead of raw acceleration, gyroscope and magnetometer data. | |||
= | [[Image:quarternion.jpg|link=]] | ||
The | Quarternions use three variables (X, Y and Z) to specify the tilt of an axis, and one additional variable (W) to specify the rotation around that axis. The main advantage of using quarternions with Phidgets is that you don't need to manually calculate heading using data from all three sensors. It also avoids problems like [https://en.wikipedia.org/wiki/Gimbal_lock#In_applied_mathematics gimbal lock] that can occur in situations where you are adding rotation angles (pitch, roll and yaw) together in real-time. Quarternions are also the preferred rotation system for programs that deal with 3D objects, like {{ARTICLE|UsingPhidgetsWithUnity|Unity}}. Quarternions are not meant to be modified directly, instead the program or library that uses them will often have functions that perform calculations using them. | ||
====How to Get Quarternions from the 1044_1==== | |||
In order to use quarternions, you need to use the {{Code|Spatial}} object instead of the individual {{Code|Accelerometer}}, {{Code|Gyroscope}} and {{Code|Magnetometer}} objects. Normally you'd use the {{Code|SpatialData}} event to have your program respond to the Phidget's motion but to get updates in quarternions, use the {{Code|AlgorithmData}} event. | |||
For | For specific function and variable names, see the {{Phidget22API|Phidget API}} for the 1044 Spatial object in the language of your choice. Here is a quick overview of the new properties and methods available: | ||
{{Code|Algorithm}} - This property allows you to choose between the AHRS and IMU algorithm (it is AHRS by default). The main difference is that IMU does not use magnetometer data, so it may perform better in applications with heavy electromagnetic noise. | |||
{{Code|AlgorithmMagnetometerGain}} - If using AHRS, you can lower the value of this property to reduce sensor noise at the cost of slowing down response time. Default value is 0.005. | |||
{{Code|zeroAlgorithm}} - This method will zero the AHRS heading to match the current reading from the compass. | |||
====Converting from Quarternions into Pitch, Roll and Yaw==== | |||
If you're not using a library that explicitly supports quarternions, you may want to convert this data into pitch, roll and yaw (also called Euler angles). The code sample below shows how you would use the x,y,z and w quarternion values to calculate pitch, roll and yaw in C#. | |||
<syntaxhighlight lang=cSharp> | |||
private void convert(Quarternion q) { | |||
double roll = (float)Math.Atan2(2f * (q.X * q.W + q.Y * q.Z), 1 - 2f * (q.X * q.X + q.Y * q.Y)); | |||
double pitch = (float)Math.Asin(2f * (q.W * q.Y - q.Z * q.X)); | |||
double yaw = (float)Math.Atan2(2f * (q.W * q.Z + q.X * q.Y), 1 - 2f * (q.Y * q.Y + q.Z * q.Z)); | |||
== | // Convert radians to degrees | ||
yaw = yaw * 180 / Math.PI; | |||
pitch = pitch * 180 / Math.PI; | |||
roll = roll * 180 / Math.PI; | |||
} | |||
< | </syntaxhighlight> | ||
You'll need a math library to perform the [https://en.wikipedia.org/wiki/Atan2 atan2] and arcsin functions. | |||
: | |||
===High Resolution Mode=== | |||
When the 1044 measures an acceleration value with magnitude less than 2g, it will acquire its data from a higher precision accelerometer chip. For these measurements, the average white noise on each axis will be reduced by approximately a factor of ten, and the resolution will increase from 976 μg to 76 μg. Likewise, when the gyroscope measures a rotation value with magnitude less than 300 °/s on the Z-axis or 400 °/s on the X or Y-axis, the noise per axis will be approximately six times lower, and the resolution will increase from 0.07 °/s to 0.02 °/s. | |||
The transition from normal to high precision or vice-versa is seamless, with no additional code or equations needed. | |||
=== | ===3-Axis Accelerometer=== | ||
The 1044 has a 3-Axis accelerometer that can measure ±8 g's (±78 m/s2) per axis. It will measure both dynamic acceleration (change in velocity) and static acceleration (gravity vector). | |||
====Orientation==== | |||
[[File:1041 0 Axis Diagram.jpg|500px|link=]] | |||
| | |||
When working with an accelerometer it is important to know which is the positive and negative direction on each of the axes. This can be determined by orienting the accelerometer along each axis and checking the output. The above image shows what the axis readings should be for each orientation of the 1044. | |||
For more information on how to use the accelerometer, check the [[Accelerometer Guide]]. | |||
===3-Axis Gyroscope=== | |||
For more information on the gyroscope, see the [[Gyroscope Guide]]. | |||
===3-Axis Magnetometer (Compass)=== | |||
The magnetometer reports the sum of all magnetic fields acting on the 1044. The earth's magnetic field is only one source that affects this measurement. In order to get accurate bearing data from the magnetometer - (i.e. to find magnetic north as a compass) any interfering magnetic effects need to be calibrated out. For more information about calibration, see the [[#Magnetic Error Correction (Calibration)|section below]], or the [[Magnetometer Guide]]. | |||
Any magnetic field that is stationary with respect to the 1044, and less than ± 3 Gauss, can be calibrated out of the magnetic field measurement. This includes both hard and soft iron effects caused by nearby ferrous and magnetic materials. Interfering magnetic fields that vary in strength and orientation with respect to the 1044 cannot be easily calibrated out. | |||
Magnetic field data will become unavailable during every other sample as the compass performs internal calibrations. When this happens, the magneticField array in the SpatialData structure will either have a length of zero, or each element will equal <code>PUNK_DBL</code>, depending on the API being used. This needs to be handled explicitly in the event handling code to avoid erroneous program behavior. The maximum sampling rate of the compass is 125 Hz. | |||
{{ | {{UGC-CompassCal}} | ||
}} | |||
For more information on magnetometers (compasses), see the [[Magnetometer Guide]]. | |||
{{UGnext|}} | |||
{{ | |||
Latest revision as of 22:03, 18 November 2024
Getting Started
Welcome to the 1044 user guide! In order to get started, make sure you have the following hardware on hand:
- 1044 Spatial Phidget
- USB cable and computer
Next, you will need to connect the pieces:

- Connect your device to your computer using the USB cable.
Now that you have everything together, let's start using the 1044!
Using the 1044
Phidget Control Panel
In order to demonstrate the functionality of the 1044, the Phidget Control Panel running on a Windows machine will be used.
The Phidget Control Panel is available for use on both macOS and Windows machines.
Windows
To open the Phidget Control Panel on Windows, find the ![]() icon in the taskbar. If it is not there, open up the start menu and search for Phidget Control Panel
icon in the taskbar. If it is not there, open up the start menu and search for Phidget Control Panel
macOS
To open the Phidget Control Panel on macOS, open Finder and navigate to the Phidget Control Panel in the Applications list. Double click on the ![]() icon to bring up the Phidget Control Panel.
icon to bring up the Phidget Control Panel.
For more information, take a look at the getting started guide for your operating system:
Linux users can follow the getting started with Linux guide and continue reading here for more information about the 1044.
First Look
After plugging the 1044 into your computer and opening the Phidget Control Panel, you will see something like this:
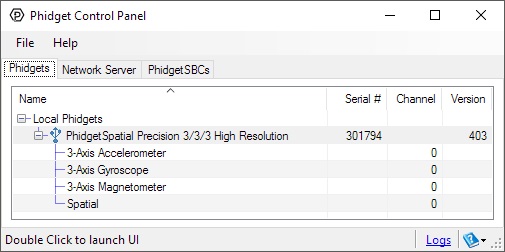
The Phidget Control Panel will list all connected Phidgets and associated objects, as well as the following information:
- Serial number: allows you to differentiate between similar Phidgets.
- Channel: allows you to differentiate between similar objects on a Phidget.
- Version number: corresponds to the firmware version your Phidget is running. If your Phidget is listed in red, your firmware is out of date. Update the firmware by double-clicking the entry.
The Phidget Control Panel can also be used to test your device. Double-clicking on an object will open an example.
Accelerometer
Double-click on the Accelerometer object in order to run the example:
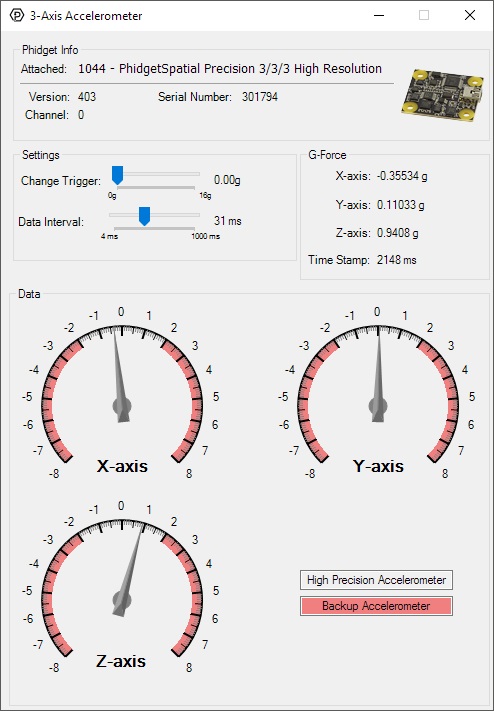
General information about the selected object will be displayed at the top of the window. You can also experiment with the following functionality:
- Modify the change trigger and/or data interval value by dragging the sliders. For more information on these settings, see the data interval/change trigger page.
- The measured values reported in g-force can be seen via labels as well as graphical dials. Try tilting the 1044 in different directions to see the labels and graphics change.
- An extremely accurate timestamp is also reported with the g-force values.
Gyroscope
Double-click on the Gyroscope object in order to run the example:
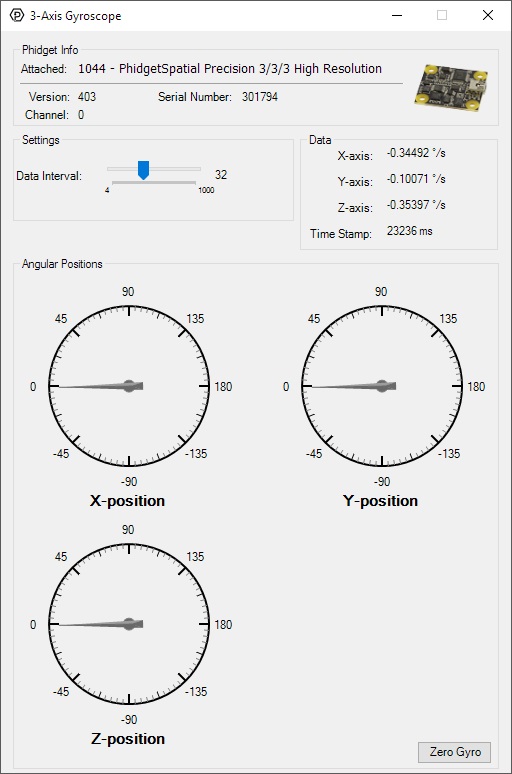
General information about the selected object will be displayed at the top of the window. You can also experiment with the following functionality:
- Modify the change trigger and/or data interval value by dragging the sliders. For more information on these settings, see the data interval/change trigger page.
- The Zero Gyro button is used to compensate for the drift that is inherent to all gyroscopes. The gyroscope primer has more information about this subject.
- The measured values reported in degrees per second can be seen via labels as well as graphical dials. Try rotating the 1044 in different directions to see the labels and graphics change.
- An extremely accurate timestamp is also reported with the g-force values.
Magnetometer
Double-click on the Magnetometer object in order to run the example:
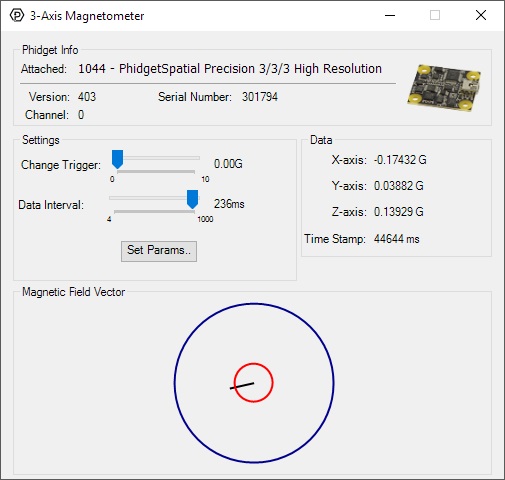
General information about the selected object will be displayed at the top of the window. You can also experiment with the following functionality:
- Modify the change trigger and/or data interval value by dragging the sliders. For more information on these settings, see the data interval/change trigger page.
- Use the Set Params... button to set the calibration parameters. For more information about calibration, see the technical section.
- The measured values reported in Gauss can be seen via labels as well as a graphical diagram. The diagram can help you visualize the magnetic field vector.
- An extremely accurate timestamp is also reported with the Gauss values.
Spatial
Double-click on the Spatial object in order to run the example:
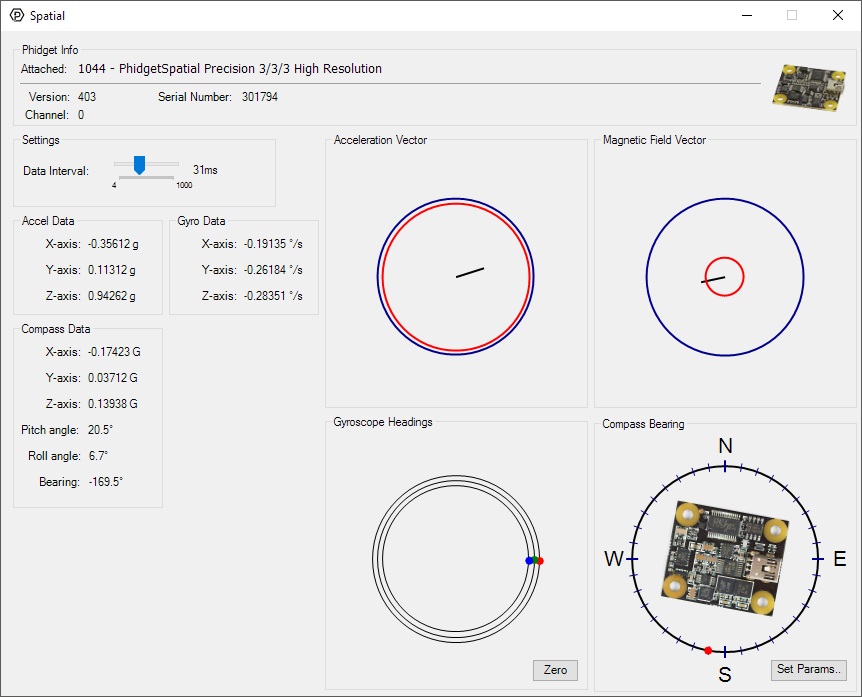
The Spatial example demonstrates that you can receive data from the accelerometer, gyroscope, and magnetometer all at once by using the Spatial object rather than the other three objects individually.
Finding The Addressing Information
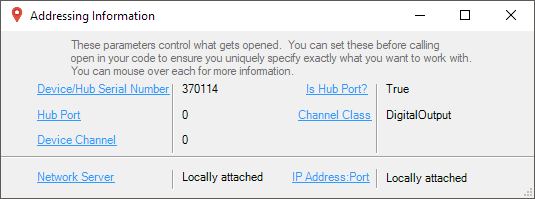
Before you can access the device in your own code, and from our examples, you'll need to take note of the addressing parameters for your Phidget. These will indicate how the Phidget is physically connected to your application. For simplicity, these parameters can be found by clicking the button at the top of the Control Panel example for that Phidget.
In the Addressing Information window, the section above the line displays information you will need to connect to your Phidget from any application. In particular, note the Channel Class field as this will be the API you will need to use with your Phidget, and the type of example you should use to get started with it. The section below the line provides information about the network the Phidget is connected on if it is attached remotely. Keep track of these parameters moving forward, as you will need them once you start running our examples or your own code.
Using Your Own Program
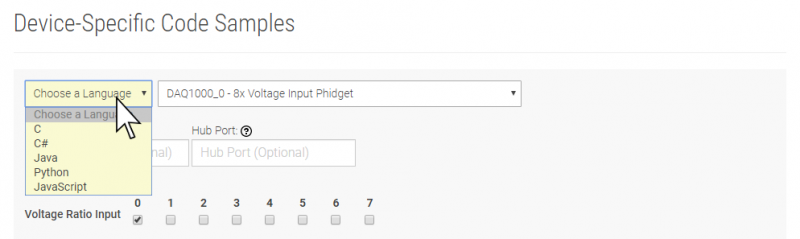
You are now ready to start writing your own code for the device. The best way to do that is to start from our Code Samples.
Select your programming language of choice from the drop-down list to get an example for your device. You can use the options provided to further customize the example to best suit your needs.
Once you have your example, you will need to follow the instructions on the page for your programming language to get it running. To find these instructions, select your programming language from the Programming Languages page.
Technical Details
Using Quarternion Algorithms
What is Quarternion?
For the 1044_1, we have added support for quarternions which can be used instead of raw acceleration, gyroscope and magnetometer data.
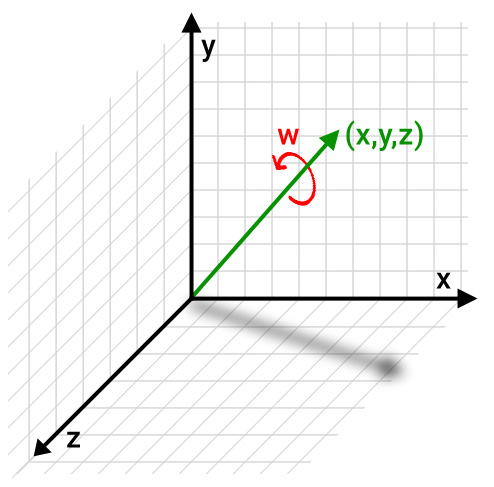
Quarternions use three variables (X, Y and Z) to specify the tilt of an axis, and one additional variable (W) to specify the rotation around that axis. The main advantage of using quarternions with Phidgets is that you don't need to manually calculate heading using data from all three sensors. It also avoids problems like gimbal lock that can occur in situations where you are adding rotation angles (pitch, roll and yaw) together in real-time. Quarternions are also the preferred rotation system for programs that deal with 3D objects, like Unity. Quarternions are not meant to be modified directly, instead the program or library that uses them will often have functions that perform calculations using them.
How to Get Quarternions from the 1044_1
In order to use quarternions, you need to use the Spatial object instead of the individual Accelerometer, Gyroscope and Magnetometer objects. Normally you'd use the SpatialData event to have your program respond to the Phidget's motion but to get updates in quarternions, use the AlgorithmData event.
For specific function and variable names, see the Phidget22 API for the 1044 Spatial object in the language of your choice. Here is a quick overview of the new properties and methods available:
Algorithm - This property allows you to choose between the AHRS and IMU algorithm (it is AHRS by default). The main difference is that IMU does not use magnetometer data, so it may perform better in applications with heavy electromagnetic noise.
AlgorithmMagnetometerGain - If using AHRS, you can lower the value of this property to reduce sensor noise at the cost of slowing down response time. Default value is 0.005.
zeroAlgorithm - This method will zero the AHRS heading to match the current reading from the compass.
Converting from Quarternions into Pitch, Roll and Yaw
If you're not using a library that explicitly supports quarternions, you may want to convert this data into pitch, roll and yaw (also called Euler angles). The code sample below shows how you would use the x,y,z and w quarternion values to calculate pitch, roll and yaw in C#.
private void convert(Quarternion q) {
double roll = (float)Math.Atan2(2f * (q.X * q.W + q.Y * q.Z), 1 - 2f * (q.X * q.X + q.Y * q.Y));
double pitch = (float)Math.Asin(2f * (q.W * q.Y - q.Z * q.X));
double yaw = (float)Math.Atan2(2f * (q.W * q.Z + q.X * q.Y), 1 - 2f * (q.Y * q.Y + q.Z * q.Z));
// Convert radians to degrees
yaw = yaw * 180 / Math.PI;
pitch = pitch * 180 / Math.PI;
roll = roll * 180 / Math.PI;
}
You'll need a math library to perform the atan2 and arcsin functions.
High Resolution Mode
When the 1044 measures an acceleration value with magnitude less than 2g, it will acquire its data from a higher precision accelerometer chip. For these measurements, the average white noise on each axis will be reduced by approximately a factor of ten, and the resolution will increase from 976 μg to 76 μg. Likewise, when the gyroscope measures a rotation value with magnitude less than 300 °/s on the Z-axis or 400 °/s on the X or Y-axis, the noise per axis will be approximately six times lower, and the resolution will increase from 0.07 °/s to 0.02 °/s. The transition from normal to high precision or vice-versa is seamless, with no additional code or equations needed.
3-Axis Accelerometer
The 1044 has a 3-Axis accelerometer that can measure ±8 g's (±78 m/s2) per axis. It will measure both dynamic acceleration (change in velocity) and static acceleration (gravity vector).
Orientation
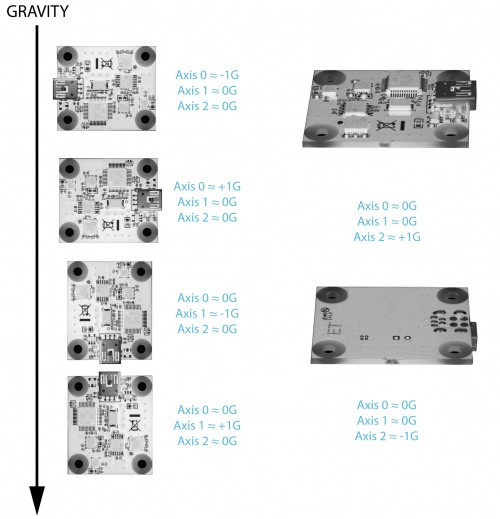
When working with an accelerometer it is important to know which is the positive and negative direction on each of the axes. This can be determined by orienting the accelerometer along each axis and checking the output. The above image shows what the axis readings should be for each orientation of the 1044.
For more information on how to use the accelerometer, check the Accelerometer Guide.
3-Axis Gyroscope
For more information on the gyroscope, see the Gyroscope Guide.
3-Axis Magnetometer (Compass)
The magnetometer reports the sum of all magnetic fields acting on the 1044. The earth's magnetic field is only one source that affects this measurement. In order to get accurate bearing data from the magnetometer - (i.e. to find magnetic north as a compass) any interfering magnetic effects need to be calibrated out. For more information about calibration, see the section below, or the Magnetometer Guide.
Any magnetic field that is stationary with respect to the 1044, and less than ± 3 Gauss, can be calibrated out of the magnetic field measurement. This includes both hard and soft iron effects caused by nearby ferrous and magnetic materials. Interfering magnetic fields that vary in strength and orientation with respect to the 1044 cannot be easily calibrated out.
Magnetic field data will become unavailable during every other sample as the compass performs internal calibrations. When this happens, the magneticField array in the SpatialData structure will either have a length of zero, or each element will equal PUNK_DBL, depending on the API being used. This needs to be handled explicitly in the event handling code to avoid erroneous program behavior. The maximum sampling rate of the compass is 125 Hz.
For more information on magnetometers (compasses), see the Magnetometer Guide.
What to do Next
- Programming Languages - Find your preferred programming language here and learn how to write your own code with Phidgets!
- Phidget Programming Basics - Once you have set up Phidgets to work with your programming environment, we recommend you read our page on to learn the fundamentals of programming with Phidgets.